Prof. dr hab. Krzysztof Goździewski oraz dr hab. Cezary Migaszewski, prof. UMK z Instytutu Astronomii opublikowali swoje ostatnie wyniki w artykule "An Exact, Generalized Laplace Resonance in the HR 8799 Planetary System" (Astrophysical Journal Letters, 2020, 902, id. L40). Jest to rezultat wieloletnich badań, które pozwoliły na znalezienie stabilnej i zgodnej z obserwacjami konfiguracji orbitalnej układu czterech masywnych planet krążących wokół gwiazdy HR 8799.
Układ HR 8799 jest pierwszym wieloplanetarnym układem pozasłonecznym odkrytym techniką bezpośredniego obrazowania, co oznacza, że planety obiegające gwiazdę HR 8799 rzeczywiście obserwujemy. Inaczej jest w przypadku metod pośrednich (np. prędkości radialnych lub tranzytów), w których to o istnieniu planet wnioskuje się na podstawie obserwacji gwiazdy, samych planet natomiast nie widząc.
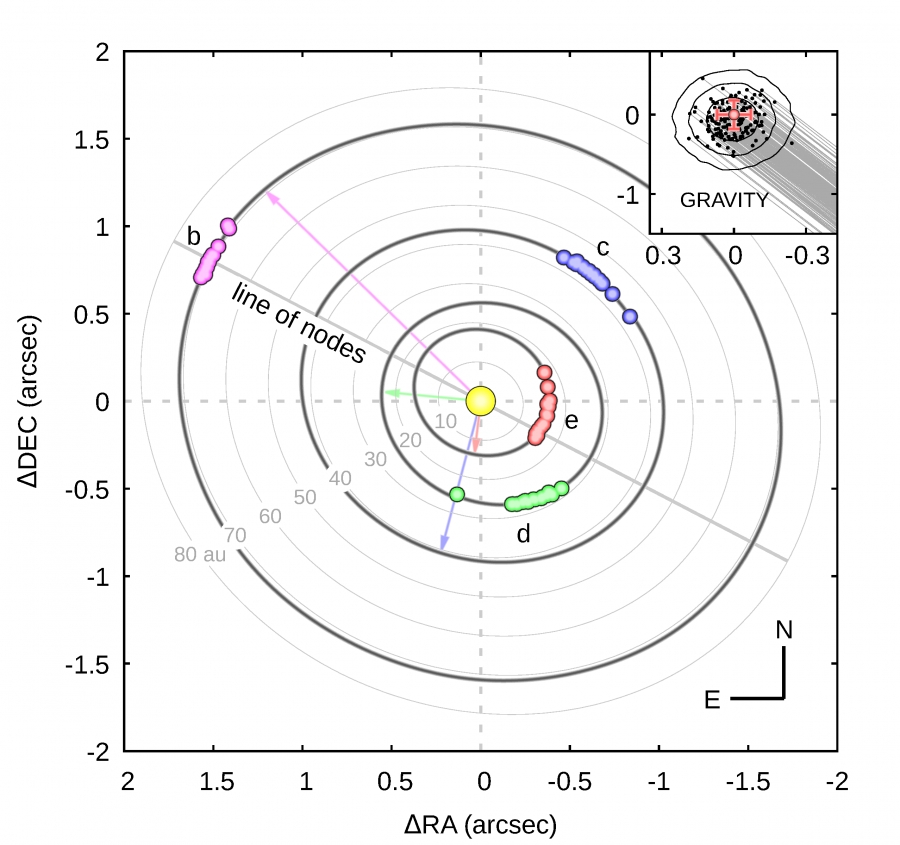
W 2008 roku odkryto trzy planety [1] w odległościach 68, 38 i 24 jednostek astronomicznych od gwiazdy macierzystej (planety te oznaczono kolejno literami b, c oraz d), z kolei dwa lata później doniesiono o odkryciu czwartej planety (oznaczonej literą e) w odległości 15 jednostek astronomicznych [2]. Masy wszystkich planet wyznaczono na od kilku do kilkunastu mas Jowisza.
Układ ten praktycznie natychmiast wzbudził duże zainteresowanie wśród astronomów zajmujących się planetami pozasłonecznymi. Naturalnym powodem takiego stanu rzeczy było to, że HR 8799 to pierwszy znany układ tego typu. Równie istotnym powodem były jednak trudności związane z wyznaczeniem parametrów orbitalnych tego systemu, a nic tak nie przyciąga uwagi naukowców jak wymagające problemy.
Odkryte planety znajdują się w dużych odległościach od gwiazdy, zatem ich okresy orbitalne są bardzo długie. Dla najbliższej planety e jest to około 50 lat, dla najodleglejszej planety b – około 450. Dane obserwacyjne pokrywają jednak znacznie krótsze przedziały czasu. Obecnie jest to około 10 lat dla planety e oraz około 20 lat dla pozostałych planet. Bezpośrednio po odkryciu układu danych było, naturalnie, jeszcze mniej. Nawet pomimo dużej precyzji obserwacji, niepewności wyznaczonych parametrów orbitalnych były olbrzymie.
Drugim problemem były duże masy planet oraz zwartość układu. To ostatnie może być nieintuicyjne, mówimy przecież o orbitach, których rozmiary mierzymy w dziesiątkach jednostek astronomicznych. Chodzi tutaj jednak o stosunki tych rozmiarów, czyli również o stosunki okresów orbitalnych. Okres planety b równy jest w przybliżeniu dwóm okresom planety c, podobnie okres planety c to około dwa okresy planety d, wreszcie okres planety d równy jest około dwóm okresom planety e. Biorąc pod uwagę całą czwórkę planet, ich okresy orbitalne są blisko stosunku 8:4:2:1. Współmierność okresów orbitalnych nazywana jest rezonansem ruchów średnich, a w przypadku, gdy w rezonansie znajduje się więcej niż jedna para planet, mówimy o łańcuchu rezonansów. Znanym przykładem konfiguracji tego typu w Układzie Słonecznym jest system księżyców Jowisza – Ganimedes, Europa i Io, których okresy orbitalne są w stosunku 4:2:1.
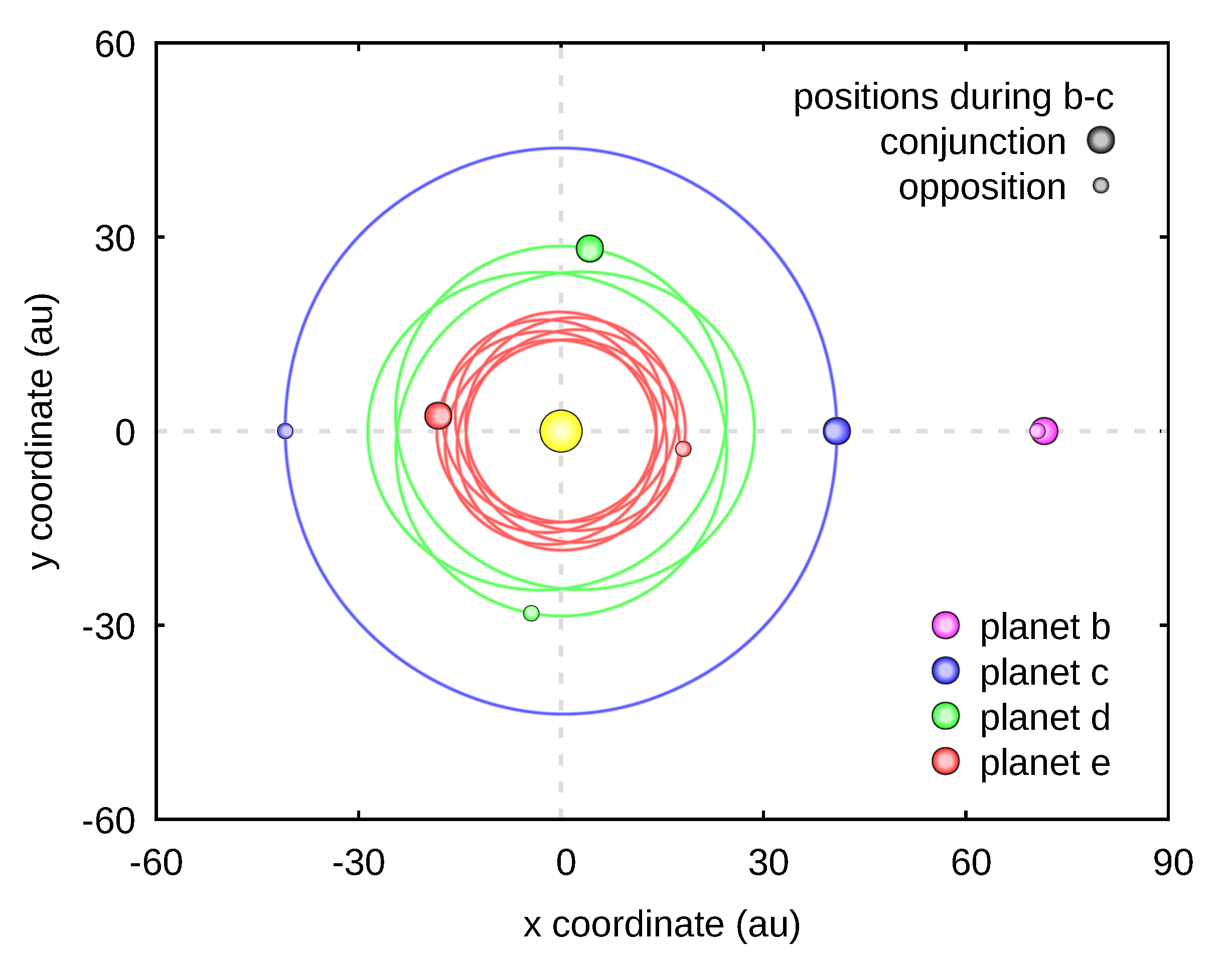
Planety wchodzące w skład układu wieloplanetarnego zaburzają wzajemnie swoje ruchy. Jeśli planety są masywne, zaburzenia te są duże. Dodatkowo, w przypadku współmierności okresów orbitalnych, zaburzenia mogą się kumulować, a to może prowadzić do destabilizacji systemu, czyli np. do wyrzucenia jednej z planet z układu, zderzenia planety z gwiazdą lub zderzenia pomiędzy planetami.
Krótko po ogłoszeniu odkrycia trzech pierwszych planet okazało się, że konfiguracje orbitalne, które dobrze pasują do danych obserwacyjnych, rozpadają się w czasie setek tysięcy lat [3]. Z uwagi na stosunkowo młody wiek gwiazdy, tj. kilkadziesiąt milionów lat, początkowo rozważana była również hipoteza mówiąca, że układ rzeczywiście rozpadnie się w niedalekiej przyszłości [4], co w skali astronomicznej oznacza czas rzędu dziesiątek milionów lat. Była to jednak w dużej mierze próba ratowania sytuacji, wydawałoby się, bez wyjścia. Problem stabilności układu stał się jeszcze trudniejszy po odkryciu czwartej planety.
Paradoksalnie, rozwiązaniem problemu okazało się być to, co było jego źródłem – rezonans ruchów średnich. Współmierność okresów orbitalnych może, ale nie musi, prowadzić do destabilizacji. Warunkiem stabilizacji jest jednak odpowiednia synchronizacja ruchów planet. Inaczej mówiąc, układ musi się znajdować w dokładnym rezonansie (inaczej nazywanym konfiguracją okresową), a nie w pobliżu rezonansu. W przypadku masywnych planet bliskość rezonansu odpowiada ewolucji niestabilnej, natomiast jedynie w niewielkim zakresie parametrów wokół konfiguracji okresowej ruch planet jest stabilny.
Obszar ten jest niezwykle mały, o wiele mniejszy niż zakres dopuszczalnych przez obserwacje parametrów. Prawdopodobieństwo znalezienia stabilnego układu pośród możliwych konfiguracji pasujących do obserwacji planet HR 8799 można porównać, nieco żartobliwie, do prawdopodobieństwa wygrania w totolotka i to w sytuacji, gdy nie gramy, a zwycięski kupom znajdujemy przypadkowo na ulicy. Istotnie, przez kilka lat po odkryciu planet nie udawało się znaleźć stabilnych konfiguracji, chociaż czas życia części z nich mógł wynosić nawet miliard lat.
Jednym ze sposobów na znalezienie stabilnej konfiguracji pasującej do obserwacji było wykorzystanie zjawiska migracji planet na skutek oddziaływania z dyskiem protoplanetarnym. Migracja zbieżna, tj. taka, podczas której planeta zewnętrzna migruje w kierunku gwiazdy szybciej niż planeta wewnętrzna, prowadzi do powstawania rezonansów ruchów średnich [5]. Fakt ten został wykorzystany do znalezienia konfiguracji rezonansowych, a następnie spośród dużej grupy takich systemów wybrano te, które poprawnie opisują dane obserwacyjne [6]. Jest to w zasadzie odwrócenie klasycznej metody, w której to najpierw szuka się układów pasujących do obserwacji, a następnie spośród nich wybiera się konfiguracje stabilne.
Podejście opisane w artykule [6] okazało się skuteczne, jednak można je było jeszcze udoskonalić. Jednym z problemów powyższej metody jest to, że szukanie konfiguracji rezonansowych jako rezultatu końcowego migracji jest bardzo wymagające obliczeniowo (obliczenia zajmują dużo czasu). Co istotniejsze jednak, metoda ta prowadzi do uzyskania niepełnego zbioru konfiguracji, co z kolei utrudnia określenie niepewności wyznaczenia parametrów orbitalnych.
Konfiguracje okresowe mogą być znajdowane również bez odwoływania się do procesu migracji, ponieważ układy takie ewoluują w szczególny sposób. Układ startując z danego punktu w przestrzeni parametrów powraca do tego punktu po pewnym skończonym czasie, nazywanym okresem. Konfiguracje takie mogą być znajdowane w procesie numerycznego całkowania równań ruchu jako funkcje mas planet oraz stosunku okresów wybranej pary planet. Mówimy wtedy, że konfiguracje okresowe tworzą w przestrzeni parametrów hiperpowierzchnię o wymiarze niższym niż wymiar tej przestrzeni.
Przykładem hiperpowierzchni jest sfera (czyli powierzchnia dwuwymiarowa) zanurzona w przestrzeni trójwymiarowej. Gdybyśmy wiedzieli skądinąd, że interesujące nas układy (dokładniej: ich reprezentacja w przestrzeni parametrów) znajdują się na sferze, to nie ma powodu przeszukiwać całej przestrzeni trójwymiarowej, a można skupić się właśnie na tej sferze. Chociaż w rozpatrywanym zagadnieniu dotyczącym układu HR 8799 przestrzeń parametrów ma znacznie więcej wymiarów niż trzy, a hiperpowierzchnia jest bardzo skomplikowana, zasada działania metody opartej o konfiguracje okresowe jest dokładnie taka jak w przykładzie ze sferą.
Metoda wykorzystująca konfiguracje okresowe została opisana w artykule [7]. Pozwoliła ona na wyznaczenie parametrów układu HR 8799 wraz z niepewnościami. Okazało się jednak, że założenie konfiguracji okresowych jako dopuszczalnych typów układów wiąże kształty orbit, jak również prędkości ruchów planet na orbitach do tego stopnia, że możliwe było poprawne wyznaczenie odległości do układu (czyli około 129 lat świetlnych) niezależnie od pomiarów paralaksy heliocentrycznej. W ogólności podejście to pozwala również na niezależne wyznaczenie mas planet, jednak aby to zrobić, potrzeba dodatkowych, precyzyjnych obserwacji.
W układzie mogą znajdować się nieznane dotąd planety, zarówno wewnątrz orbity planety e, jak i na zewnątrz orbity planety b. Poszukiwania trwają. Pomocne mogą okazać się tutaj badania dysków, składających się z małych obiektów, takich jak asteroidy czy planetoidy. Ich rozmieszczenie w systemie może być określone dzięki podczerwonej emisji pyłu, powstałego podczas zderzeń tych obiektów [8]. Z drugiej strony, dodatkowa, nieobserwowana jeszcze planeta, oddziałując grawitacyjnie, formuje strukturę takich dysków [9]. Połączenie wyników powyższych analiz może wskazać potencjalne obszary w układzie, gdzie takie dodatkowe planety mogą istnieć.
Literatura:
[1] Marois i in. 2008, Science, 322, 1348, doi:10.1126/science.1166585
[2] Marois i in. 2010, Nature, 468, 1080, doi:10.1038/nature09684
[3] Fabrycky i Murray-Clay, 2010, ApJ, 710, 1408, doi:10.1088/0004-637X/710/2/1408
[4] Goździewski i Migaszewski, 2009, MNRAS, 397, L16, doi:10.1111/j.1745-3933.2009.00674.x
[5] Snellgrove, Papaloizou i Nelson, 2001, A&A, 374, 1092, doi:10.1051/0004-6361:20010779
[6] Goździewski i Migaszewski, 2014, MNRAS, 440, 3140, doi:10.1093/mnras/stu455
[7] Goździewski i Migaszewski, 2020, ApJL, 902, L40, doi:10.3847/2041-8213/abb881
[8] Booth i in., 2016, MNRAS, 460, L10, doi:10.1093/mnrasl/slw040
[9] Goździewski i Migaszewski, 2018, ApJS, 238, id 6, doi:10.3847/1538-4365/aad3d3

 Grudziądzka 5, 87-100 Toruń
Grudziądzka 5, 87-100 Toruń